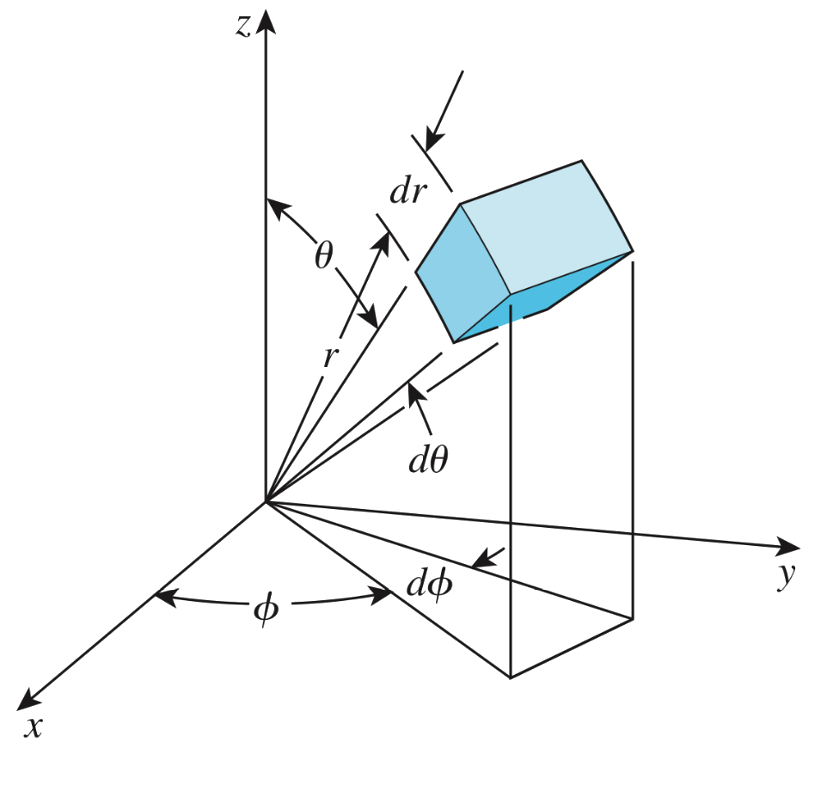
MATH 22: Introduction to Calculus of Several Variables
(Summer 2025)
- Welcome to the course webpage for the Summer 2025 (Session 2) manifestation of MATH 22: Introduction to Calculus of Several Variables at the University
of California, Santa Cruz.
Course Info
- Summer 2025 (Session 2)
- 5:00PM - 7:15PM M/W/F
- Cowell 131
- 5 Credits
Instructor Info
- Jadyn V. Breland (he/him/his)
- 4:45PM-5:45PM Tu/Th
- McHenry 4117
| Course Syllabus | Reading Assignments | Daily Assignments & Notes | Weekly Assignments | Edfinity Exercises | Exam Info |
Welcome!
- You've reached the course web page for the Summer 2025 manifestation of MATH 22: Introduction to Calculus of Several Variables at the University of California, Santa Cruz.
Purpose and Goals:
-
The primary objective of this course is to help students become confident and competent in solving problems using the techniques of multivariable calculus.
Broadly speaking, multivariable calculus is the study of functions that depend on two or more variables. Such functions arise naturally in many contexts,
especially in describing the physical world.
We will explore these functions through tools such as differentiation and integration. By the end of the course, students will understand the geometry of Euclidean space--including how to describe points, lines, and planes--and will have developed fluency with limits and continuity. Students will learn to differentiate and integrate a wide range of functions, and apply these skills to problems involving approximation, optimization, surface area, volume, arclength, curvature of space curves, and more.
Beyond content mastery, a central aim of this course is to support your development as an independent learner. While learning calculus is valuable, even more valuable is the ability to reason logically from first principles and to communicate your conclusions clearly and convincingly. I hope you'll also experience one of the great joys of mathematics: the deep satisfaction that comes with truly understanding something.
An Active Learning Approach:
-
This is not a lecture-driven course, nor one where mimicking prefabricated examples will ensure success. You'll be expected to actively build your own understanding of the material,
with support from me,
our TA, and your classmates.
Many of the problems and ideas we'll encounter will be unfamiliar and will challenge you to think in new ways. You will experience frustation and failure,
before you experience understanding. This all a part of the normal learning process. In short, if you are doing things well, you should be confused at different points over the next five weeks. The material is too rich for a human
being to completely understand it immediately.
In this course, we will incorporate ideas from an educational philosophy called active learning. Active learning refers to any instructional method that engages students in the learning process. This style of teaching and learning contrasts sharply with the traditional mathematics lecture, where the instructor talks and students (attempt to) passively recieve information.“A good lecture is usually systematic, complete, precise—and dull; it is a bad teaching instrument.”
There is a great deal of recent scholarship that suggests that students learn better when they are actively engaged in the learning process. You can not master the electric guitar by watching Buckethead shred, nor can you become a chess grandmaster by watching Magnus Carlson on twitch. In a similar fashion, you cannot master calculus by simply watching; you must do calculus!
--Paul R. Halmos"Mathematics is not a spectator sport."
Therefore, a significant portion of our time in class meetings will be reserved for doing calculus in a supportive and collaborative environment. We will be using the free and open-source textbook Active Calculus: Multivariable written by Steve Schlicker. Active calculus is riddled with activities that will form the backbone of our course. To prepare for class meetings, you will complete Reading Assignments which typically include reading assigned sections of the text, completing "Preview Activities", completing other activities or questions, and writing down some things you learned or questions you still have. During class, we will spend the significant majority of the time working through the Activities in Active Calculus, usually in small groups. These are the Daily Assignments. Outside of class, you will have ample opportunity to improve your understanding of calculus by solving low-stakes Edfinity Exercises and to demonstrate fluency by writing coherent solutions to substantial calculus problems in the Weekly Assignments.
--George Pólya