Alejandro Bravo-Doddoli.
“Life is good for only two things: doing mathematics and teaching it.” -Simeon Poisson.
Biography.
“May slavery be banished forever, as well as the distinction between castes, all remaining equal.” -Jose María Morélos y Pavón, liberator of the Americas.
Research
Non-integrable distributions, sub-Riemannian geometry, non-holonomics mechanics, Carnot Groups, Integrable and chaotic sub-Riemannian goedesic flow.
Biography
I am currently a Ph.D. student at the University of California Santa Cruz and advised under Dr. Richard Montgomery.
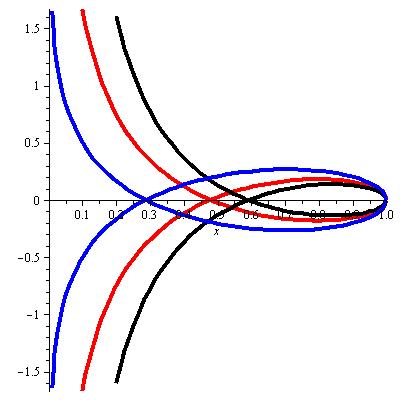
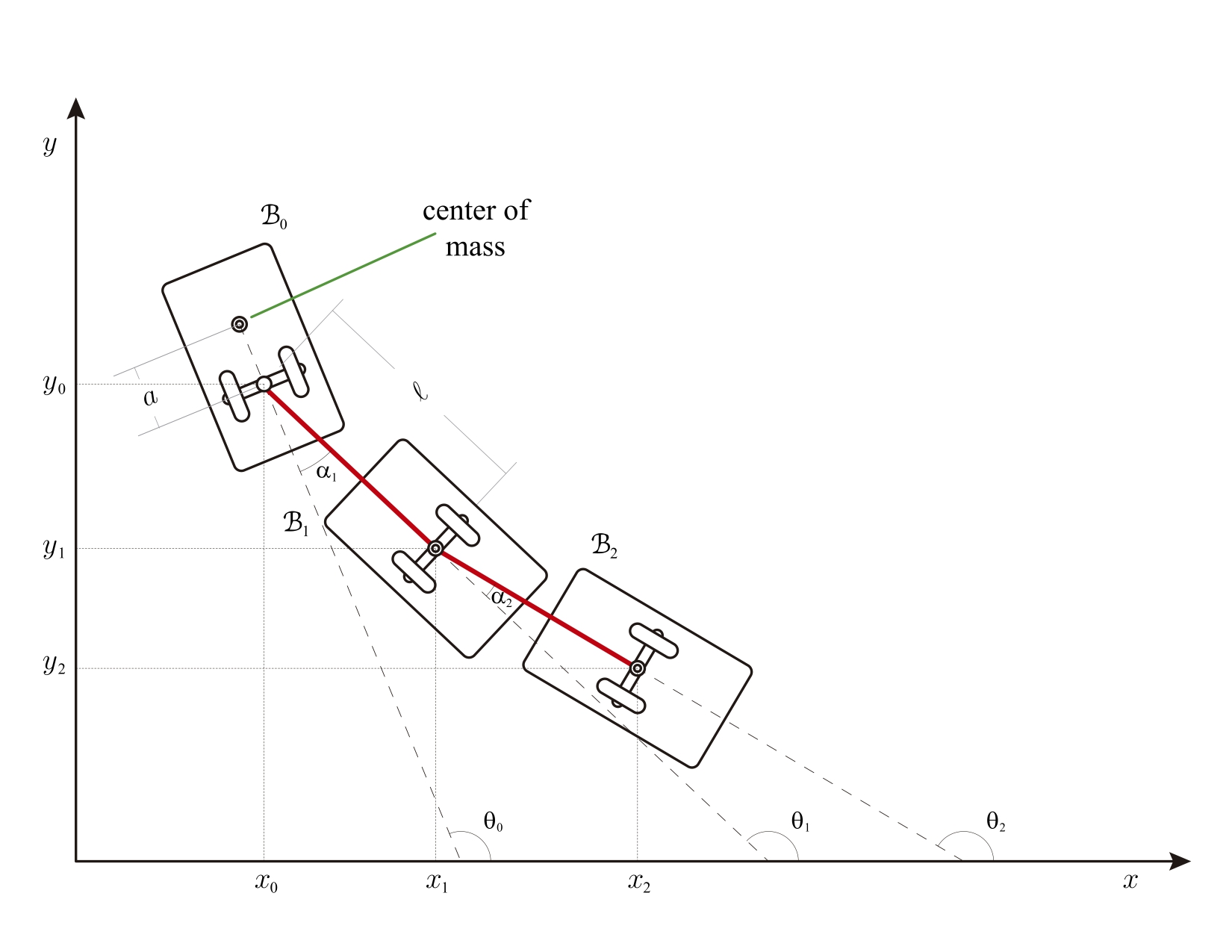
The n-trailer vehicle. Watch some simulations.
The n-trailer vehicle has been an interesting topic in three different areas of the mathematics; non-holonomics mechanics, Goursat distribution theory from the point of view of the differential topology, and the moster tower from the point of view of algebraic geometry
Luis Garcia-Narajo and I studied the dynamics of an articulated n-trailer vehicle that moves under its own inertia. Learn more
Graduate Colloqum at Mathematic depamernt UCSC.
The graduate students of the UCSC Mathematics Department has talks every Monday from 4-5 PM. Colloquium website
In-person talks will be in McHenry 4130 and will have a 30m tea (drinks and snacks) in McHenry 4161 beforehand. Remote talks will have a meet-and-greet ~15m before the talk. By Zoom: 971 7015 4206 Passcode: 766123. Direct link.
The following talk is in person on March 6th by Changhan Zou from UCSC: Tensor-triangular classification and support theories.
We will review some classical classification theorems in algebraic geometry, modular representation theory, and stable homotopy theory, through the lens of tensor triangular geometry. Then we will discuss various support theories developed for the purpose of classifying "big" objects. In particular, we will clarify the relation between the support theory of Benson-Iyengar-Krause, and the support theory of Balmer-Favi, for rigidly-compactly generated tensor-triangulated categories..
CV, talks, training and teaching.
I was graduate student instructor at Facultad de Ciencias at UNAM and I attend to “Preparing for Inclusive Teaching” at UCSC’s C.I.T.L. (Center for Innovations in Teaching and Learning) (2017-2021).View details
