Coordinated Math 216 website
This first place to look for any information is RIGHT HERE, consider looking it up any time you have any question. If the answer is not on there, feel free to email.The remainder of this page contains some information and notes specific to the sections I am teaching, i.e. 030 and 040.
General info
Lectures: MWF 10:00-11:00am (sec. 30) and 11:00am-noon (sec. 40), 260 WEISER.Office hours: (open to all sections)
- François Monard: MW 1-2:30pm, all in the Math Lab.
- Gracie Ingermanson (GSI, 30): M 3-4pm, F 11am-noon, EH 4852. Th 12-1pm Math Lab.
- Jeremy West (GSI, 40): H 1-4pm, Math Lab.
- Jennifer Park (Instructor, 10-20): MW 3-4pm, EH 3060. Th 7-8pm Math Lab.
- Bradley Rogers (Instructor, 50-60): M 3-4pm, F 4-5pm, EH 1863. M 7-8, Math Lab.
- Xiaolin Wang (Instructor, 70): TW 3:30-5pm, EH 1846. F 11am-noon, Math Lab.
Additional Material
- 01/22/2016: lecture7, Euler's method
- 01/25/2016: lecture8, comparison of numerical schemes
- 01/27/2016: lecture9, an example of bifurcation
- 01/27/2016: some recap notes
- 02/24/2016: vector-valued ODE's
- 03/23/2016: almost linear systems: The two examples below illustrate cases where the linearized system fails at capturing the non-linear one (Cases 1 and 2 in Theorem 2 of section 6.2).
Consider the system \[ \binom{x}{y}' = \binom{-y + \mu (x^2+y^2)x}{x + \mu (x^2+y^2)y}, \] where $\mu$ is a parameter varying between $-0.5$ and $0.5$ in the picture. In this example, the linearized system has matrix $\left[ \begin{smallmatrix} 0 & -1 \\ 1 & 0 \end{smallmatrix}\right]$ for every $\mu$, with eigenvalues $\pm i$. As predicted, while the linearized system (see fig. right) cannot tell whether the corresponding non-linear critical point is a sink, center or source, the nonlinear system (fig. left) gives all possible outcomes depending on the value of $\mu$ (center at $\mu=0$, sink for $\mu<0$, source for $\mu>0$). 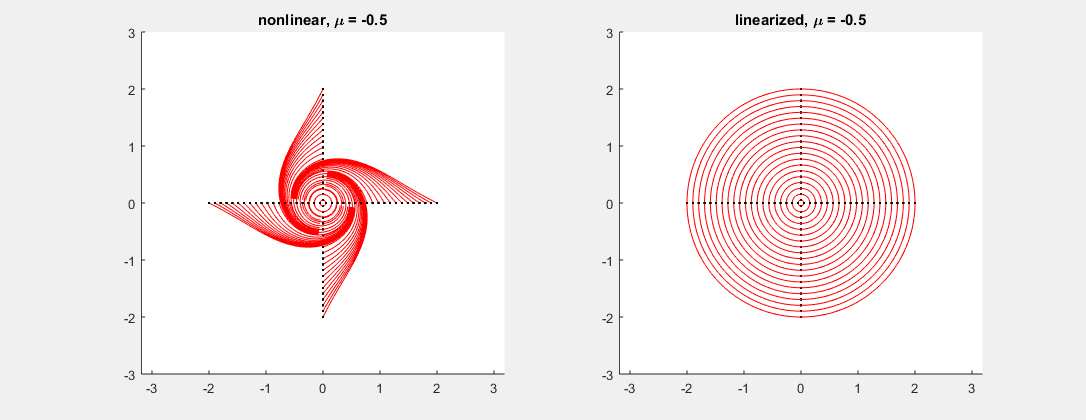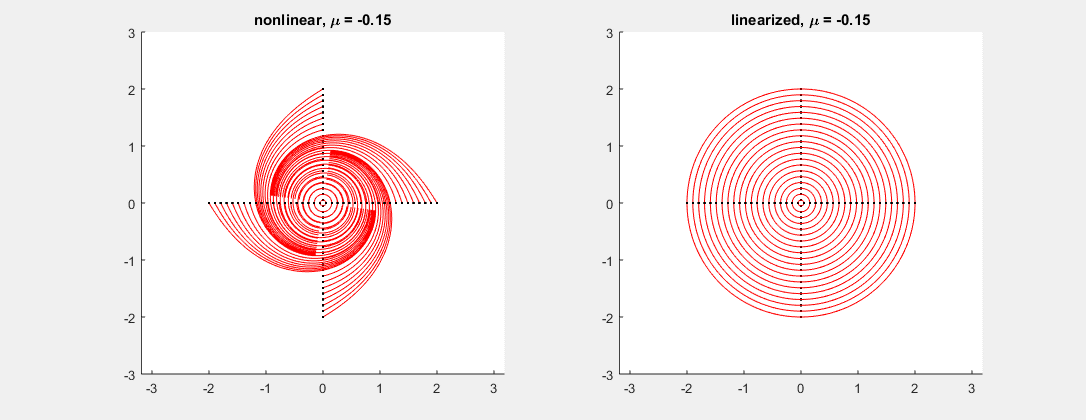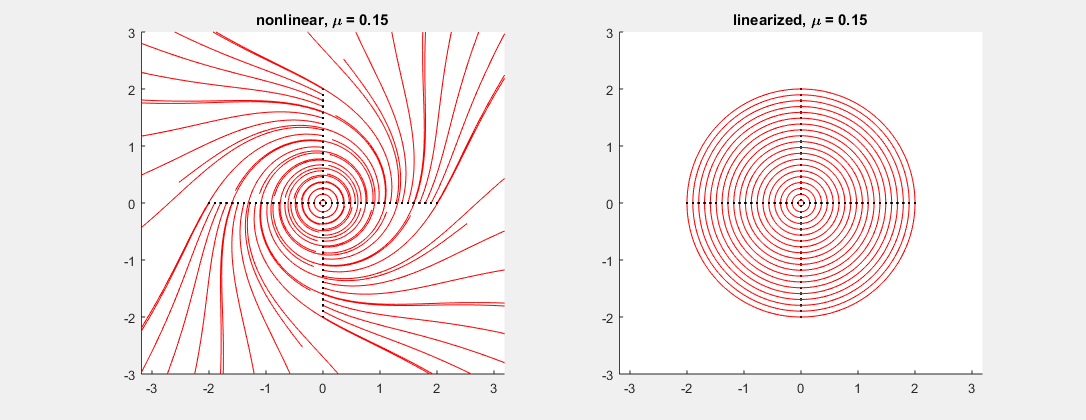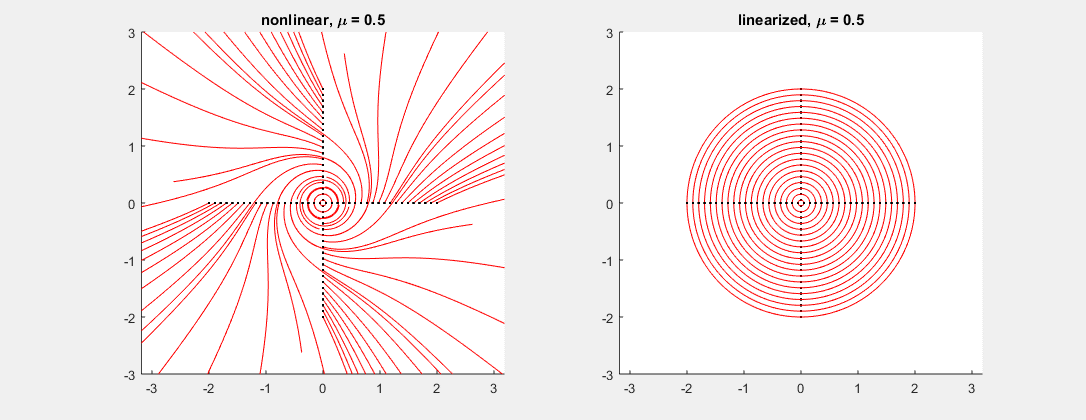
Consider the system \[ \binom{x}{y}' = \binom{-x - \mu (x^2+y^2)y}{-y + \mu (x^2+y^2)x}, \] where $\mu$ is a parameter varying between $-0.5$ and $0.5$ in the picture. In this example, the linearized system has matrix $\left[ \begin{smallmatrix} -1 & 0 \\ 0 & -1 \end{smallmatrix}\right]$ for every $\mu$, with double eigenvalue $-1$. As predicted, while the linearized system (see fig. right) cannot tell whether the corresponding non-linear critical point is a node or a spiral, the nonlinear system (fig. left) gives all possible outcomes depending on the value of $\mu$ (node at $\mu=0$, spiral otherwise). 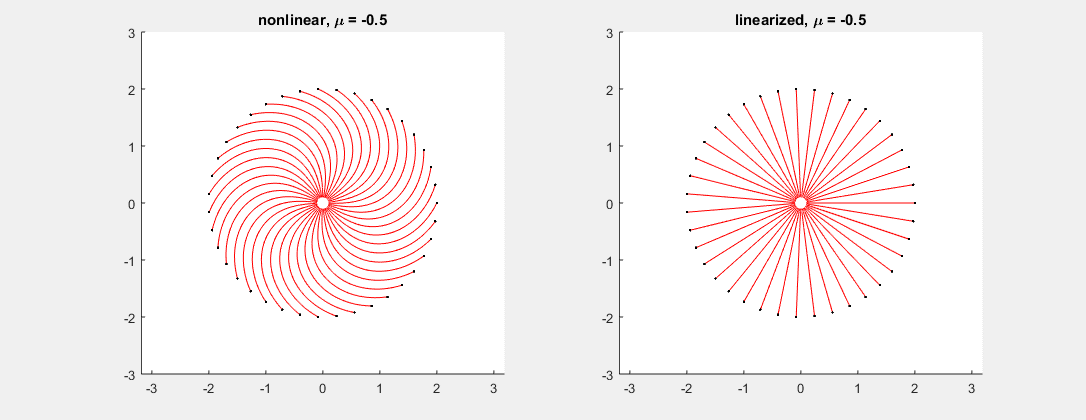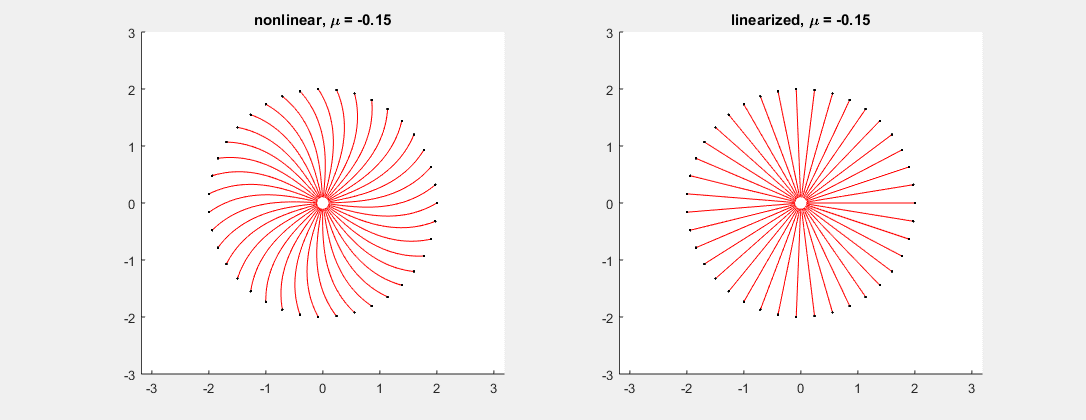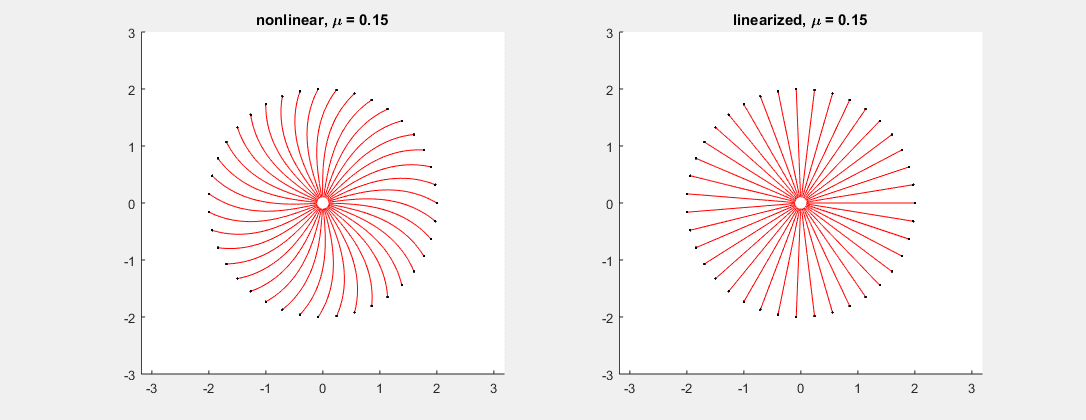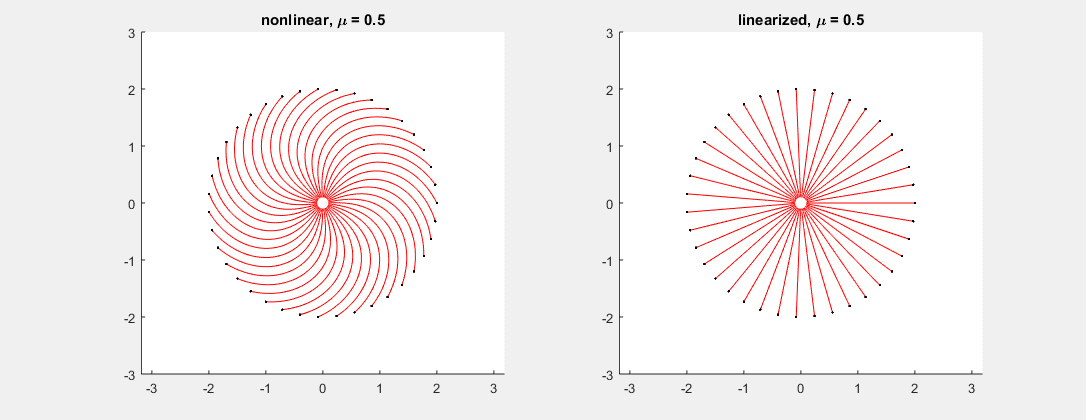
- 03/30/2016: dynamical systems, chaos and fractals
- Review sheet on phase plane analysis and polynomials