Navigation
Home
Group
Publication
Research
Teaching
Media
Service
Album
Misc
Opening

Big Picture

The landscape and word cloud visualization of my research thrusts and PhD thesis:

landscape_tag. 


Here are a number of research projects that I have been working on.

Power System State Estimation

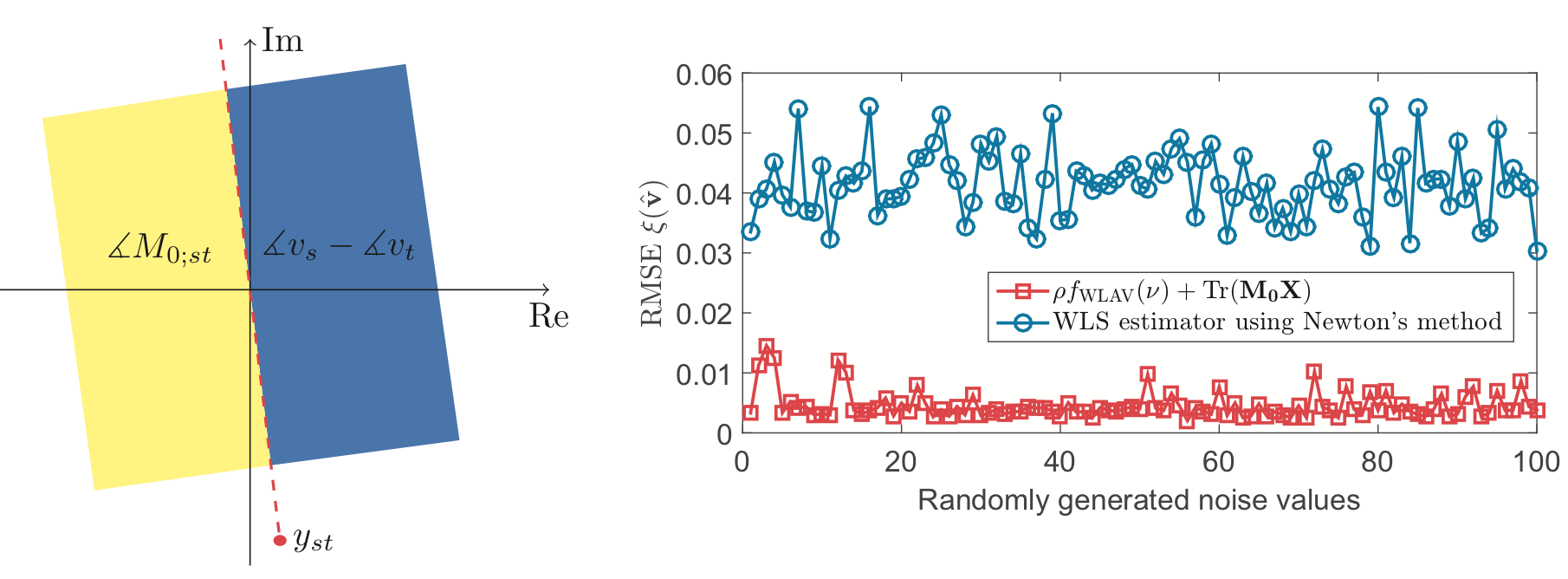angle conditions and the comparison with Newton method 

Left figure: The acceptable regions for the voltage phase difference (blue open half space), and the entry of coefficient matrix (yellow open half space) are shown relative to the line admittance (red dot).

Right figure: The root-mean-square errors of the estimated voltages obtained by the proposed method and the weighted least squares based Newton method for the IEEE 118-bus system.


Research challenges:
1. How to deal with the non-convex optimization problem formulated for the state estimation?
2. How good is the performance of convexification ? Contributions: We propose a convexification framework based on semidefinite programming (SDP) and second-order cone programming (SOCP) relaxations to cope with inherent non-convexity of power flow (PF) and power system state estimation (PSSE) problems. We study the performance of the proposed framework in the case where the set of measurements includes: (i) nodal voltage magnitudes, and (ii) branch active power flows over a spanning tree of the network. It is shown that the SDP and SOCP relaxations both recover the true PF solution as long as the voltage angle difference across each line of the network is not too large. By capitalizing on the result for the PF problem, penalized SDP and SOCP problems are designed to solve the PSSE. Strong theoretical results are derived to quantify the optimal solution of the penalized SDP problem, which is shown to possess a dominant rank-one component formed by lifting the true voltage vector. An upper bound on the estimation error is also derived as a function of the noise power, which decreases exponentially fast as the number of measurements increases. Related paper:

Robust and Stochastic Energy Management with High-Penetration Renewables

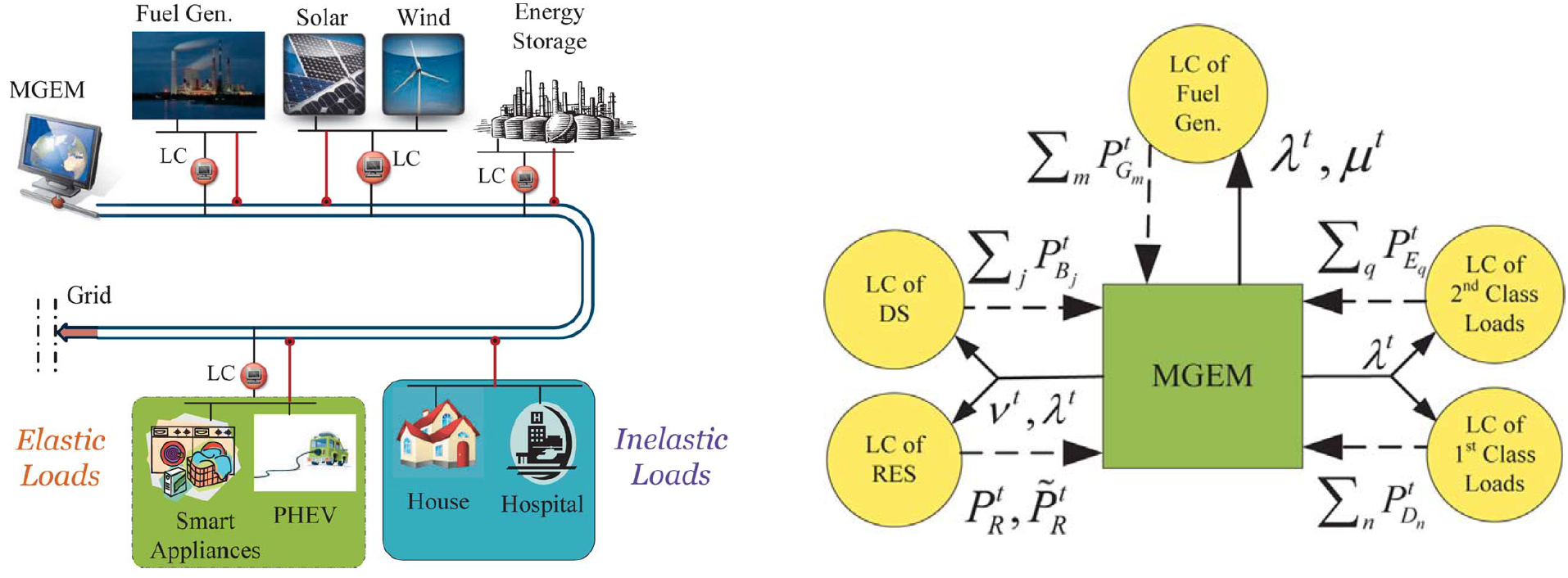Distributed control and computation architecture of a microgrid 

Left figure: Typical infrastructure of a microgrid with distributed energy resources.

Right figure: Primal-dual message passing architecture of distributed computations leveraging the dual decomposition.


Research challenges:
1. How to handle the inherent uncertainty of renewable energy sources for day-ahead market clearing and power dispatch?
2. How to engage all local controllers in the distributed energy management for microgrids? Contributions: Due to its reduced communication overhead and robustness to failures, distributed energy management is of paramount importance in smart grids, especially in microgrids, which feature distributed generation (DG) and distributed storage (DS). To address the intrinsically stochastic availability of renewable energy sources (RES), a novel power scheduling approach is introduced. The approach involves the actual renewable energy as well as the energy traded with the main grid, so that the supply–demand balance is maintained. Leveraging the dual decomposition, the optimization problem formulated is solved in a distributed fashion by the local controllers of DG, DS, and dispatchable loads. Capitalizing on the conditional value-at-risk (CVaR), the novel day-ahead stochastic market clearing model is able to mitigate the potentially high risk of the recourse actions to compensate wind forecast errors. The resulting convex optimization task is tackled via a distribution-free sample average based approximation to bypass the prohibitively complex high-dimensional integration. Furthermore, to cope with possibly large-scale dispatchable loads, a fast distributed solver is developed with guaranteed convergence using the alternating direction method of multipliers (ADMM). Related papers:

Energy Data Analytics

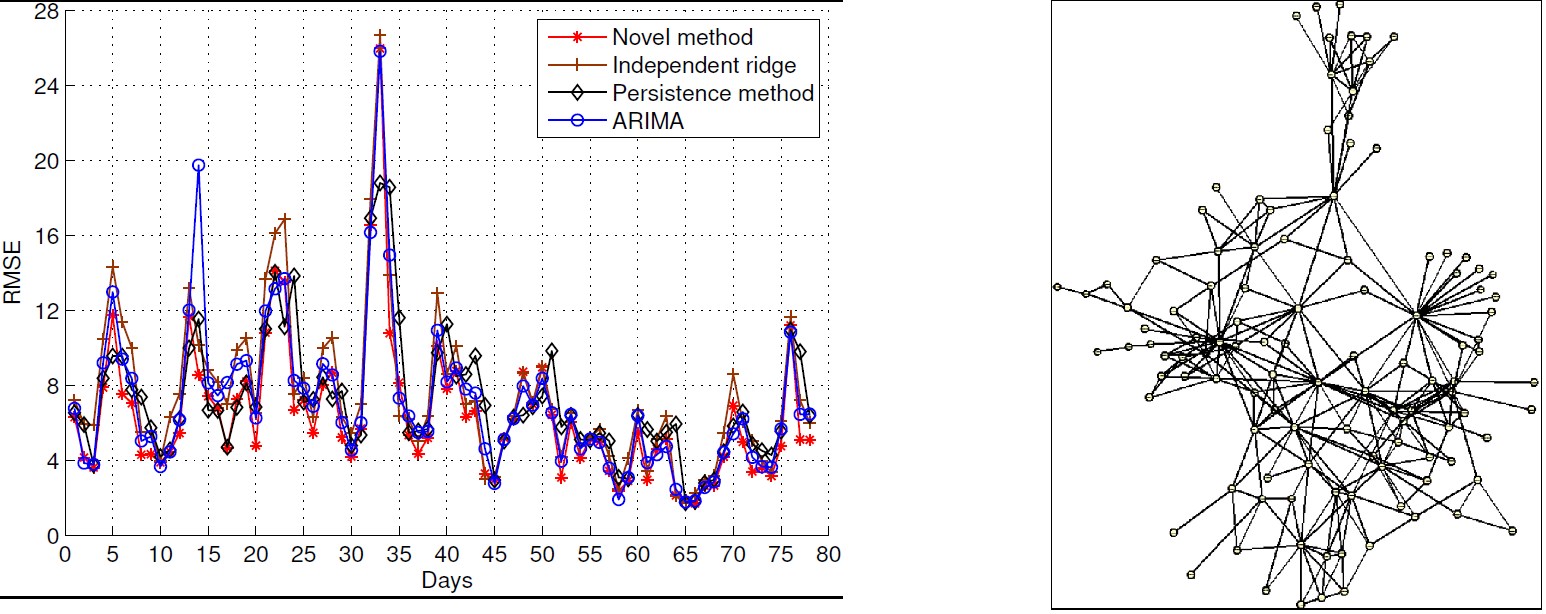Electricity price forecasting for the MISO Summer 2012 market 

Left figure: Root-mean-square error comparison of different forecasting methods.

Right figure: Graph of the local balancing authorities (LBAs) involved in the MISO market.


Research challenges:
1. How to exploit the valuable spatio-temporal correlations in energy data (electricity prices, load demand, renewable power generation, etc)?
2. How to develop fast and scalable algorithms for massive datasets? Contributions: The smart grid vision entails advanced information technology and data analytics to enhance the efficiency, sustainability, and economics of the power grid infrastructure. Aligned to this end, modern statistical learning tools are leveraged for electricity market inference. Day-ahead price forecasting is cast as a low-rank kernel learning problem. Uniquely exploiting the market clearing process, congestion patterns are modeled as rank-one components in the matrix of spatio-temporally varying prices. Through a novel nuclear norm-based regularization, kernels across pricing nodes and hours can be systematically selected. Even though market-wide forecasting is beneficial from a learning perspective, it involves processing high-dimensional market data. The latter becomes possible after devising a block-coordinate descent algorithm for solving the non-convex optimization problem involved. The algorithm utilizes results from block-sparse vector recovery and is guaranteed to converge to a stationary point. Related papers:

Big Data Sketching

Data sketching 

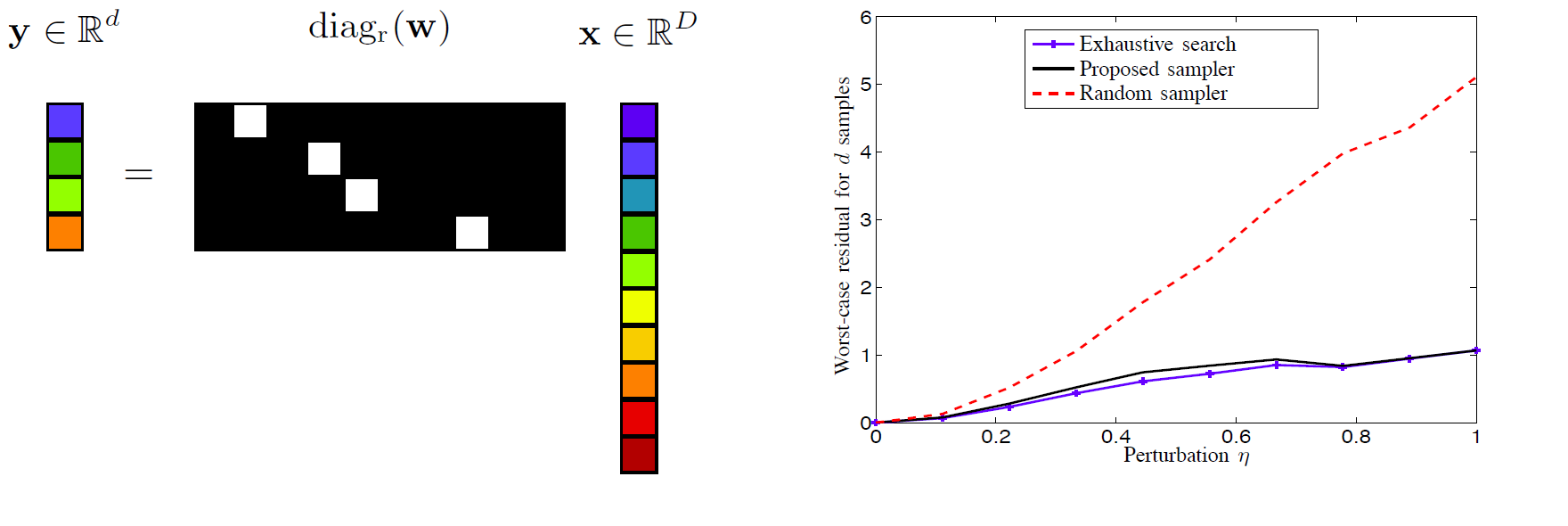Left figure: Sparse sketching scheme for data reduction: A white (black) and colored square represents a one (zero) and an arbitrary value, respectively.

Right figure: Worst-case residual comparison of different sampling schemes with respect to various perturbation values.


Research challenges:
1. How to design efficient samplers for big data sketching robust to model uncertainties? Abstract: Data reduction for large-scale linear regression is one of the most important tasks in this era of data deluge. Exact model information is however not often available for big data analytics. We propose a framework for big data sketching (i.e., a data reduction tool) that is robust to possible model mismatch. Such a sketching task is cast as a Boolean min-max optimization problem, and then equivalently reduced to a Boolean minimization program. Capitalizing on the block coordinate descent algorithm, a scalable solver is developed to yield an efficient sampler and a good estimate of the unknown regression coefficient. Related paper:

Optimal Resource Allocation for Green Communications and Geo-Distributed Data Centers

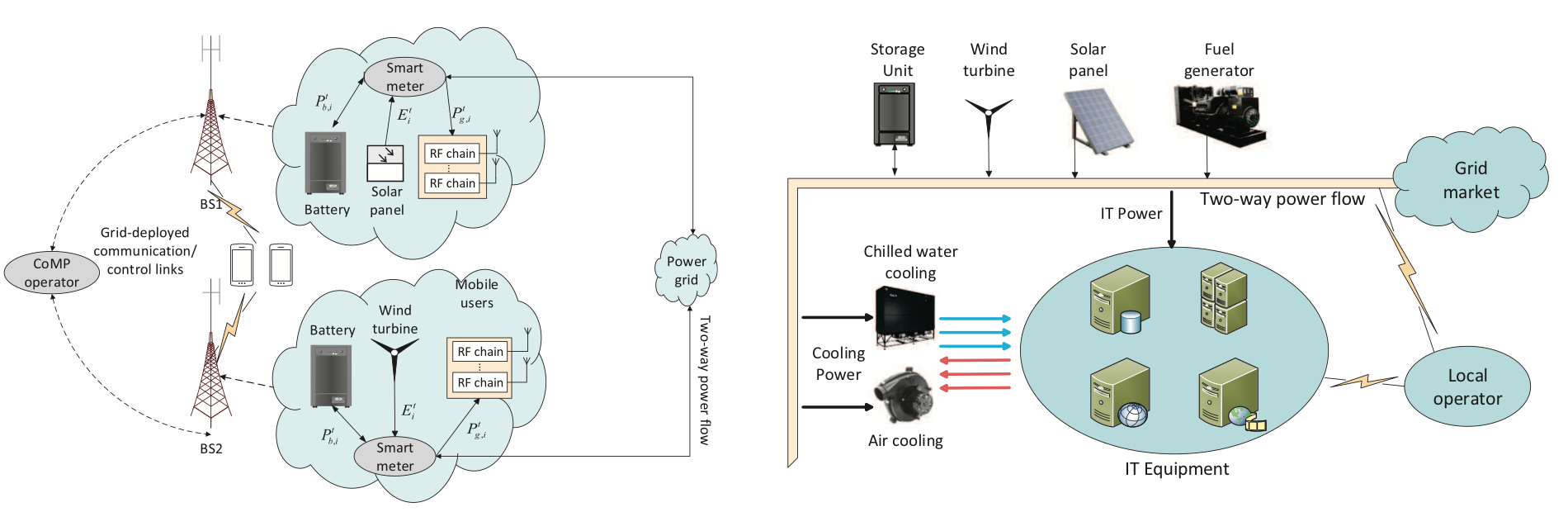A smart grid powered CoMP system and a cloud network of geo-distributed DCs 

Left figure: A smart-grid-powered coordinated multi-point system.

Right figure: A smart-grid-powered sustainable data center.


Research challenges:
1. How to systematically incorporate clean energy sources to support the green and sustainable operations of wireless communication systems and geo-distributed data centers?
2. What is the impact of uncertainties of renewable energy on the ahead-of-time and real-time decision making? Contributions: We develop dynamic energy management for smart-grid powered coordinated multi-point (CoMP) transmissions. To address the intrinsic variability of renewable energy sources, a novel energy transaction mechanism is introduced for grid-connected base stations that are also equipped with an energy storage unit. Aiming to minimize the expected energy transaction cost while guaranteeing the worst-case users’ quality of service, an infinite-horizon optimization problem is formulated to obtain the optimal downlink transmit beamformers that are robust to channel uncertainties. Capitalizing on the virtual-queue based relaxation technique and the stochastic dual-subgradient method, an efficient online algorithm is developed yielding a feasible and asymptotically optimal solution. A large number of geo-distributed data centers begin to surge in the era of data deluge and information explosion. To meet the growing demand in massive data processing, the infrastructure of future data centers must be energy-efficient and sustainable. Facing this challenge, a systematic framework is put forth to integrate renewable energy sources (RES), distributed storage units, cooling facilities, as well as dynamic pricing into the workload and energy management tasks of a data center network. To cope with RES uncertainty, the resource allocation task is formulated as a robust optimization problem minimizing the worst-case net cost. Related papers:

Optimal Transceiver Design for Wireless Communication Networks

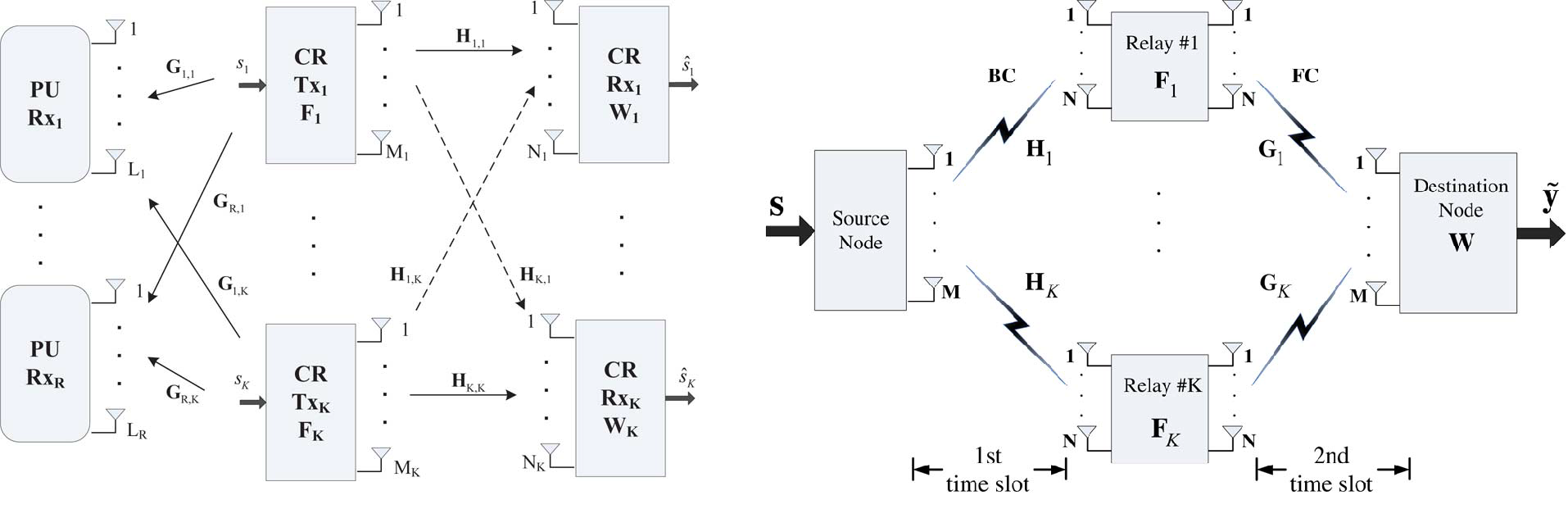The system models for MIMO ad hoc CR and dual-hop networks 

Left figure: System model for multi-input multi-output (MIMO) ad-hoc cognitive radio networks.

Right figure: Dual-hop MIMO network with relay beamforming.


Research challenges:
1. How to improve the spectrum efficiency and transmission reliability for cognitive radio systems?
2. How to systematically reduce channel interference to guarantee the end-users’ quality of service?
3. How to simultaneously achieve the distributed array and intra-node array gains for a relay network? Abstract: We optimize the design of transmit- and receive-beamformers for ad hoc CR networks when CR-to-CR channels are known, but CR-to-PU channels cannot be estimated accurately. Capitalizing on a norm-bounded channel uncertainty model, the optimal beamforming design is formulated to minimize the overall mean-square error (MSE) from all data streams, while enforcing protection of the PU system when the CR-to-PU channels are uncertain. Even though the resultant optimization problem is non-convex, algorithms with provable convergence to stationary points are developed by resorting to block coordinate ascent iterations, along with suitable convex approximation techniques. Enticingly, the novel schemes also lend themselves naturally to distributed implementations. Related papers: