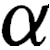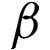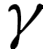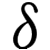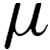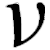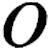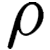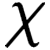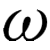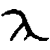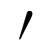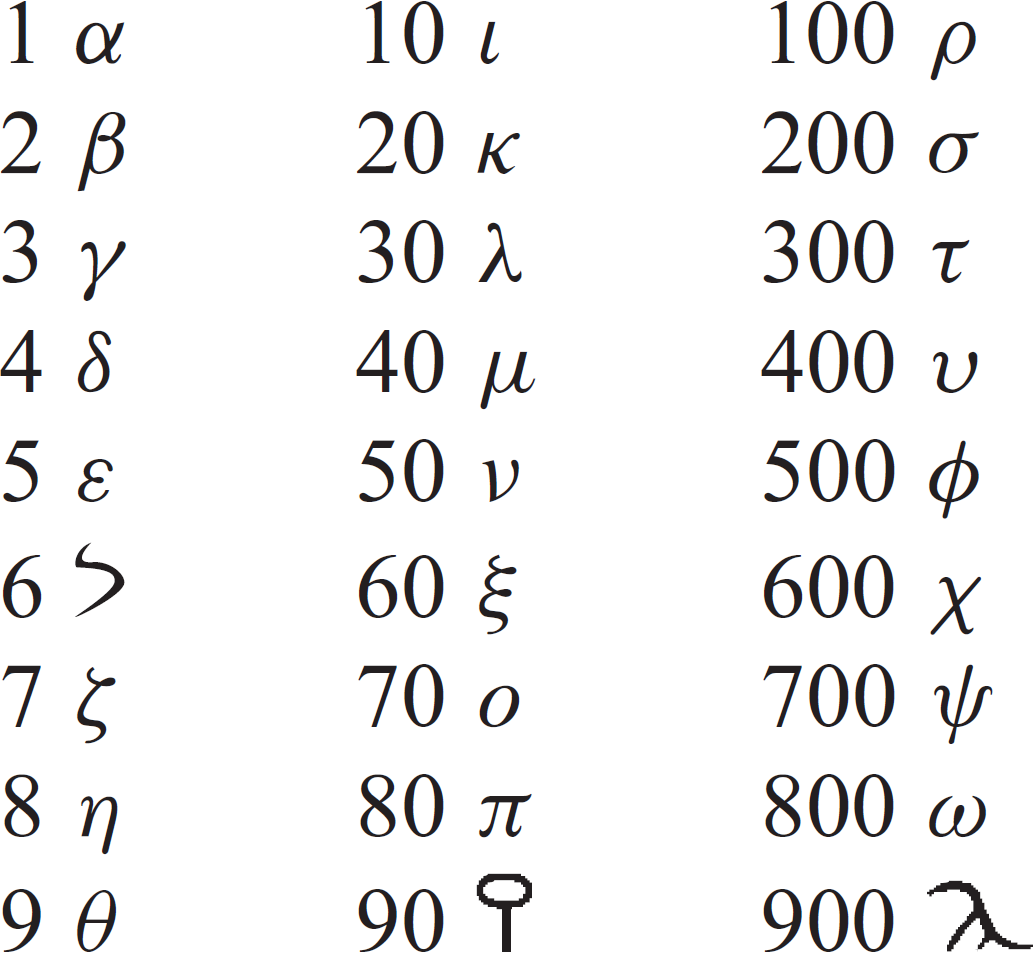Instructions

Enter a number in the first box by additively clicking on the 1 or the 10 symbol (e.g. to get 3, click the 1 symbol 3 times). Your number is displayed in base 60, just as the Babylonians wrote their numbers.

Press an operator button.

Enter the next number into the second box just as you did the first.

Press solve to view your solution.

Press the clear button to start over.

Babylonian Math

The Babylonians used a positional number system, which allowed them to represent nearly any number, no matter how large or small. Unlike our number system, the Babylonians represented numbers in base 60, so every number increases its value by a factor of 60 as you move left.

Though large and small numbers could be represented, not having a symbol for zero left the number system with much ambiguity without context. This is why the calculator above uses an additive system for input. It would be impossible to parse the input accurately without this system, as there could be several interpretations of the number entered. This ambiguity is also why the calculator does not work with fractions, and can only divide when the result is an integer.

(Source, pg 16)

Instructions

Enter the number in the first box by entering in the Ionian Greek number.
Press an operator button.
Enter the next number into the second box just as you did the first.
Press solve to view your solution.
Press the clear button to start over.

Ionian Greek Math

The Greeks of Ionia used an alphabetic numeral system. That is, each symbol of the Greek alphabet combined with three Phoenician letters were used to denote a number, as shown in the table above. They used an additive system, in that the value of each symbol in a string of symbols was added together to get a number.

To represent numbers larger than 999, the Greeks of Ionia placed an accent mark before a symbol to multiply it by 1,000, and placed an after a symbol or set of symbols to multiply it by 10,000.