COVID-19 Guatemala
Descripción del Modelo
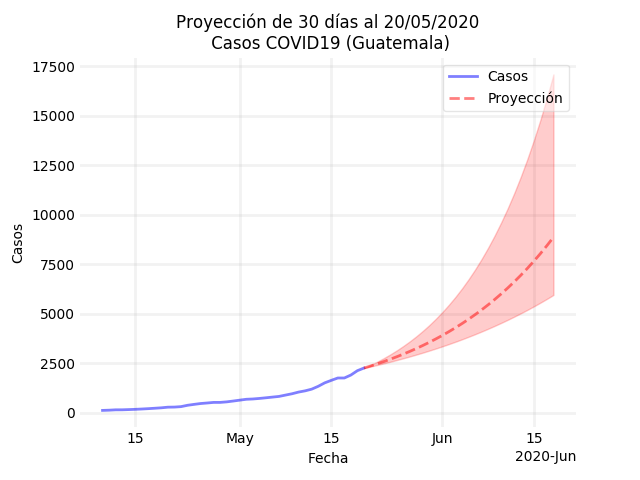
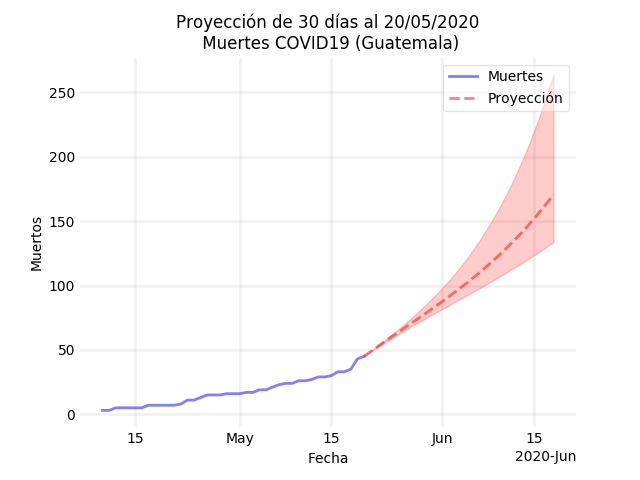
¿Cómo se obtiene la proyección?
Descripción
Se utiliza un modelo compartimentado aprendido con datos de los 14 días anteriores al inicio de la proyección. Los parámetros y la ventana de tiempo se calculan minimizando errores de interpolación con base a los datos reportados.
Modelo Compartimentado
Estas proyeciones se basan en un modelo compartimentado ajustado con datos reales. En este modelo se asumen cinco compartimentos:
- Susceptibles: Total de personas que pueden contraer la enfermedad.
- Expuestos: Personas que han estado en contacto con un infectado, desarrollarán síntomas, y serán detectados por el sistema.
- Diagnosticados: Personas que están contagiadas, han realizado una prueba y han dado positivo.
- Recuperados: Personas que estuvieron contagiadas y se han recuperado de la enfermedad.
- Muertos: Personas que estuvieron contagiadas y han muerto debido a la enfermedad.
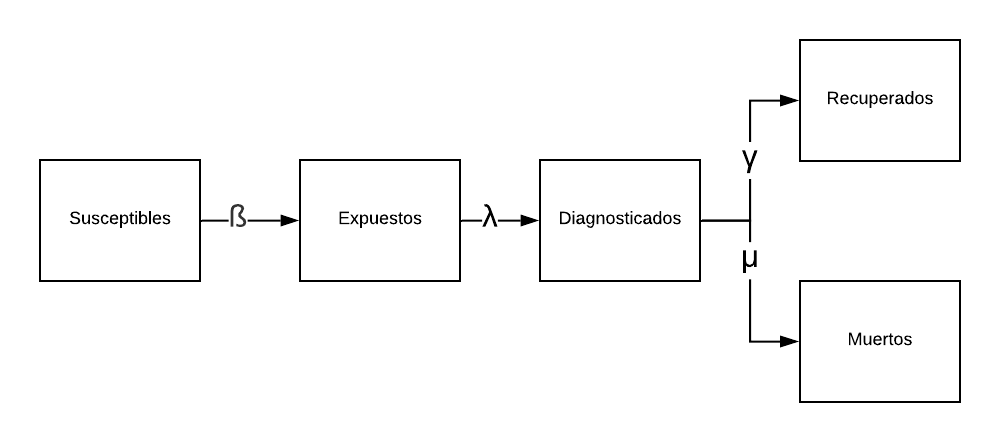
Tomando como \(S(t), E(t),I(t),R(t),D(t)\) el número de susceptibles, expuestos, diagnosticados, recuperados y muertos respectivamente, tenemos que el modelo compartimentado viene dado por el sistema de ecuaciones diferenciales, $$ \begin{eqnarray} S'(t)&=&-\beta\frac{E(t)}{N}S(t)\\ E'(t)&=&\beta \frac{E(t)}{N}S(t)-\lambda E(t)\\ I'(t)&=&\lambda E(t)-\gamma (1-\mu ) I(t)-\gamma \mu I(t)\\ R'(t)&=&\gamma (1-\mu ) I(t)\\ D'(t)&=&\gamma \mu I(t) \end{eqnarray} $$ dónde los parámetros del modelo son,
- \(\beta\): Tasa de contagio del virus. Se calcula a través de los datos utilizando el valor del número de reproducción \(R_t\), obteniendo también intervalos de confianza.
- \(\lambda\): Tasa de latencia del virus. Es igual a \(1/\text{tiempo de latencia}\). El tiempo de latencia es el tiempo en días que una persona infectada contagia a otras personas. Dada la poca disponibilidad de datos, este parámetro es comunmente estimado por el período de incubación, el cual comprende el tiempo desde que un individuo se infecta hasta que presenta síntomas. Se obtiene de artículos publicados al respecto con intervalos de confianza.
- \(\gamma\): Tasa de recuperación. Es igual a \(1/\text{tiempo de recuperación}\). Se obtiene de artículos publicados al respecto con intervalos de confianza.
- \(\mu\): Letalidad. Se calcula a través de los datos obteniendo intervalos de confianza.
- \(N\): Número total de individuos. Se utilizan datos del censo y estimaciones actuales.
Este modelo considera que la cantidad total de individuos es constante, es decir, $$S'(t)+E'(t)+I'(t)+R'(t)+D'(t)=0\,.$$ También se considera que el brote se propaga debido a los individuos expuestos y no a los diagnosticados, ya que se asume que los diagnosticados han sido puestos en cuarentena u hospitalización y por ende ya no pueden seguir contagiando. También se asume que los recuperados desarrollan una inmunidad y que no van a contagiarse de nuevo (al menos durante un perído que no afecta al brote).
Número de reproducción
Se toma el número de reproducción efectivo como el promedio de contagios secundarios en una ventana de tiempo. Este número efectivo captura medidas de contención y sanitarias, por lo que cambia en el tiempo.
Para calucular este, se recurren a dos métodos: 1) la matriz de generación y 2) la ecuación de Lotka–Euler.
Matriz de generación
Esta describe el flujo de infectados entre compartimentos cerca del punto de equilibrio libre de infecciones. Para esto, se consideran solamente los compartimentos que contienen individuos infectados. En este caso, se tiene que flujo de infectados puede ser expresado como, $$\frac{d X(t)}{d(t)}=\mathcal{F}(t)-\mathcal{V(t)}\,,$$ donde \(X(t)=\left(E(t), I(t)\right)\) es el vector de compartimentos con individuos infectados. El vector \(\mathcal{F}\) da la tasa de entrada de nuevos infectados a cada compartimiento infeccioso y el vector \(\mathcal{V}\) da la tasa de transición entre los compartimientos infecciosos.
Con los Jacobianos de \(\mathcal{F},\mathcal{V}\), $$F=D(\mathcal{F})\,,\qquad V=D(\mathcal{V})\,,$$ se obtiene la matriz de generación, la cual está dada por $$FV^{-1}\,.$$ Esta matriz da el número esperado de nuevos infectados. Se tiene que el radio espectral, es decir, el valor propio más grande, da el valor del número de reproducción efectivo, $$R=\rho(FV^{-1})\,.$$ En este caso se tiene que en el equilibrio sin infecciones, \(S=N\) y por lo tanto, $$ \begin{eqnarray} \mathcal{F}&=&\left(\beta E,0 \right)\\ \mathcal{V}&=&\left(\lambda E,-\lambda E+\gamma I \right)\\ \end{eqnarray} $$ lo que da $$ F=\begin{pmatrix} \beta & 0\\ 0&0 \end{pmatrix}\,,\qquad V=\begin{pmatrix} \lambda & 0\\ -\lambda &\gamma \end{pmatrix} $$ por lo que $$ FV^{-1}=\begin{pmatrix} \frac{\beta}{\lambda} & 0\\ 0&0 \end{pmatrix}\,, $$ y $$R=\rho(FV^{-1})=\frac{\beta}{\lambda}\,.$$
Ecuación de Lotka–Euler
El intervalo generacional es el tiempo entre una infección primaria y una secundaria. Estos tiempos varían ente individuos por lo que es posible generar una distribución de tiempos \(g(\tau)\). Con esto se obtiene que el número de reproducción efectivo está dato por, $$R=\left(\int g(\tau)\frac{i(t-\tau)}{i(t)}\,d\tau\right)^{-1}\,,$$ dónde se toma la distribución sobre el intervalo considerado.
En la práctica es complicado conocer la distribución de los intervalos generacionales, ya que no se conoce exactamente cuándo fue infectado cada individuo ni cuándo y a cuántos individuos secundarios infectó. Generalmente esta distribución se aproxima con la distribución del tiempo de incubación. Es decir, el tiempo en que tarda un individuo en presentar síntomas luego de haber sido infectado.
¿Cómo se obtienen los parámetros?
Latencia \((\lambda)\)
Se estima utilizando datos de intervalos de incubación. Existen varios artículos científicos publicados a este respecto. En este modelo se considera el valor mediano de \(\lambda=5.1\) días con un intervalo de confianza de \((4.3,5.8)\) días con una confianza del 95%.
Letalidad \((\mu)\)
Utilizando los datos reportados, se obteinen las razones diarias entre muertes y diagnosticados positivos. Con estos datos se obtienen el valor medio y el intervalo de confianza al 95%.
Tasa de reproducción \((\beta)\)
Utilizando la ecuación de Lokta-Euler se calcula el número de reproducción efectivo diario con base a los 14 días previos. La ventana de tiempo se fija minimizando el error de interpolación entre el modelo y los datos. Luego se calcula este valor para cada día durante las dos semanas previas para obtener una distribución de valores. Con esto se calcula el valor medio y el intervalo de confianza al 95% para los valores de \(R\).
Utilizando la matriz de generación, se calcula \(\beta\) y su intervalo de confianza en términos de \(R\).
Manejo de errores
Bandas de Confianza
Para determinar bandas de confianza se utilizan los extremos de los intervalos de confianza para los parámetros obtenidos. Con estos se resuelve el sistema de ecuaciones diferenciales obteniendo las curvas de máximos y mínimos.
Validación
El modelo se valida realizando interpolación para los datos existentes. Para esto, se realiza una segmentación de datos en dos: 1) el conjunto de datos para entrenar el modelo y obtener los parámetros y 2) el conjunto de datos para validar el modelo. Esta validación se realiza para cada día, tomando los 14 días anteriores para entrenar el modelo y los días siguientes hasta la fecha, para validar el modelo.
La validación y aprendizaje se realizan con una función de verosimilitud logarítimica. Está viene dada por $$L_j=E\left(\log\left(\frac{f^j_i}{y_i}\right)^2\right)\,,$$ y $$L=E(L_j)\,,$$ donde \(\{f^j_i\}\) es la estimación dada para el día \(i\) por el modelo centrado en el día \(j\), \(\{y_i\}\) es el valor de los datos reales para el día \(i\) y \(E(\cdot)\) es el valor promedio.
Es posible evaluar el rendimiento general del modelo por medio de calcular el coeficiente de determinación promedio, $$R_j^2=1-\frac{\sum^j_i (y_i-f^j_i)^2}{\sum^j_i (y_i-E(y))^2}$$ y $$R^2=E(R^2_j)\,.$$
Referencias
- https://www.acc.org/latest-in-cardiology/journal-scans/2020/05/11/15/18/the-incubation-period-of-coronavirus-disease
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7081172/pdf/aim-olf-M200504.pdf
- https://www.who.int/bulletin/online_first/20-255695.pdf
- https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf
- https://www.sciencedirect.com/science/article/pii/S1755436518300847
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6002118/
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2871801/
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1766383/
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3582628/
- https://www.censopoblacion.gt/
- https://www.ine.gob.gt/ine/portal-estadistico-1-0/
- https://github.com/CSSEGISandData/COVID-19